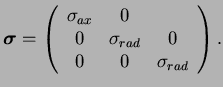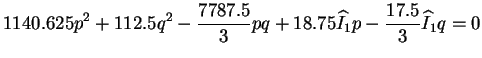suivant: Homothétie isotrope, translation cinétique
monter: Théorie plastique pour les
précédent: Théorie plastique pour les
Table des matières
L'origine de l'anisotropie est imputable d'après Oda &
al. [OO92] à l'orientation des surfaces de contact entre
particules voisines. Le matériau testé est du sable. Deux types
d'écrouissage sont ici distingués. Le premier est isotrope et
relatif à la dilatance. Le second type est relié à la distribution
des normales aux contacts. Il est possible de définir un plan
tangent au point de contact de deux grains et une normale à ce
plan ainsi que l'illustre la figure 4.5.1.
Figure 4.5.1:
Pour des géométries complexes telles que celles des grains
de poudre de fer, la normale au contact ne coïncide pas nécessairement
avec la jonction des centres. Pour des sphères, cette coïncidence est
systématique
|
|
Dans le cas de deux sphères, la normale au contact a pour
direction la droite qui relie les deux centres des sphères. Une
distribution des normales est alors décrite par une fonction
scalaire
 qui identifie la pondération relative
des contacts de normale unitaire
qui identifie la pondération relative
des contacts de normale unitaire
 dans
l'assemblage. Par définition, la distribution
dans
l'assemblage. Par définition, la distribution
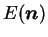 vérifie la propriété :
où
vérifie la propriété :
où 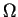 est l'angle solide égal à la surface d'une sphère de
rayon unité,
est l'angle solide égal à la surface d'une sphère de
rayon unité,
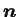 est le vecteur normal unitaire du
contact. La distribution
est le vecteur normal unitaire du
contact. La distribution
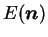 s'exprime en fonction
des termes
s'exprime en fonction
des termes 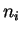 qui sont les composantes du vecteur
qui sont les composantes du vecteur
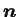 donnée par
donnée par
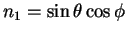 ,
,
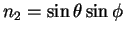 et
et
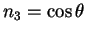 par une projection dans un
repère orthonormé.
Une propriété de cette fonction est la symétrie par rapport au
sens de la normale :
par une projection dans un
repère orthonormé.
Une propriété de cette fonction est la symétrie par rapport au
sens de la normale :
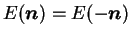 .
Une distribution isotrope et aléatoire des orientations de contact
est définie par une fonction
.
Une distribution isotrope et aléatoire des orientations de contact
est définie par une fonction
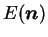 égale à une valeur
constante de
égale à une valeur
constante de 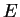 pour tout vecteur
pour tout vecteur
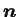 .
La valeur constante de
.
La valeur constante de 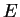 associée à une distribution aléatoire
vaut :
La fonction
associée à une distribution aléatoire
vaut :
La fonction
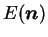 est utilisée pour définir un
tenseur de structure des contacts noté
est utilisée pour définir un
tenseur de structure des contacts noté
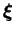 .
Les composantes
.
Les composantes 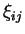 de ce tenseur de structure peuvent être
exprimées en coordonnées sphériques par :
où les termes
de ce tenseur de structure peuvent être
exprimées en coordonnées sphériques par :
où les termes 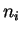 sont les composantes du vecteur
sont les composantes du vecteur
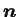 données par
données par
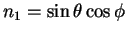 ,
,
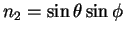 et
et
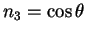 par projection dans un repère
orthonormé. Il est à noter que ce tenseur est symétrique
(
par projection dans un repère
orthonormé. Il est à noter que ce tenseur est symétrique
(
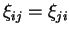 ). Une autre propriété de ce tenseur est que
sa trace est unitaire pour toute distribution
). Une autre propriété de ce tenseur est que
sa trace est unitaire pour toute distribution
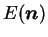 .
Dans le cas d'une distribution isotrope des orientations de
contact, il vient une forme particulière pour le tenseur de
structure :
Cette description qui tient compte en partie de la structure
microscopique a pour vocation de décrire l'établissement et
l'évolution de l'anisotropie. Un intérêt particulier doit ainsi
être porté sur les variations de contact induites par le
chargement imposé. Par considération des deux premiers invariants
du tenseur
.
Dans le cas d'une distribution isotrope des orientations de
contact, il vient une forme particulière pour le tenseur de
structure :
Cette description qui tient compte en partie de la structure
microscopique a pour vocation de décrire l'établissement et
l'évolution de l'anisotropie. Un intérêt particulier doit ainsi
être porté sur les variations de contact induites par le
chargement imposé. Par considération des deux premiers invariants
du tenseur
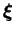 , il apparaît que les évolutions de la
structure du réseau de contact modifient seulement les valeurs du
second invariant de
, il apparaît que les évolutions de la
structure du réseau de contact modifient seulement les valeurs du
second invariant de
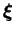 . En effet :
Ceci implique que l'incrément
. En effet :
Ceci implique que l'incrément
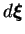 est un tenseur
déviatoire. Puisque l'évolution des contacts est due au chargement
imposé, il est alors possible de supposer que
est un tenseur
déviatoire. Puisque l'évolution des contacts est due au chargement
imposé, il est alors possible de supposer que
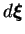 peut être relié à l'incrément de la partie déviatoire du tenseur
des contraintes. Cette supposition conduit logiquement à souligner
qu'un ensemble de grains muni d'une répartition initiale de
contact aléatoire restera aléatoire si un état de compression
isotrope lui est appliqué (les composantes
peut être relié à l'incrément de la partie déviatoire du tenseur
des contraintes. Cette supposition conduit logiquement à souligner
qu'un ensemble de grains muni d'une répartition initiale de
contact aléatoire restera aléatoire si un état de compression
isotrope lui est appliqué (les composantes 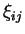 restent
égales à
restent
égales à
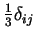 au cours de la
densification).
Par contre, pour une répartition de contact initialement aléatoire
en fin de remplissage, une direction privilégiée de contact
parallèle à l'axe de compression va s'établir au cours d'une
compression en matrice comme l'illustre la figure
4.5.2(B).
au cours de la
densification).
Par contre, pour une répartition de contact initialement aléatoire
en fin de remplissage, une direction privilégiée de contact
parallèle à l'axe de compression va s'établir au cours d'une
compression en matrice comme l'illustre la figure
4.5.2(B).
Figure 4.5.2:
Évolution de la forme des grains au cours de la
compression en matrice. (A) au remplissage, (B) en cours de
compression, (C) densification complète
|
|
Les effets de la densification sur la structure du réseau de
contacts peuvent être ainsi distingués. Le chargement isotrope et
la compression en matrice diffèrent par la valeur du second
invariant de
 (respectivement nulle et non
nulle).
Pour l'exemple de la compression en matrices, les directions
principales majeures des tenseurs de structure (
(respectivement nulle et non
nulle).
Pour l'exemple de la compression en matrices, les directions
principales majeures des tenseurs de structure (
 ) et de contraintes (
) et de contraintes (
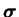 ) sont confondues. La
direction principale majeure fait référence à la direction du
vecteur propre associé à la valeur propre de valeur absolue
maximum. Pour des distributions de contacts initialement
non-aléatoires ou pour des histoires de chargements complexes, les
deux directions majeures citées ci-dessus ne coïncident pas
a priori. Afin de tenir compte de ces situations, Oda
& al. [OO92] proposent de définir un angle
) sont confondues. La
direction principale majeure fait référence à la direction du
vecteur propre associé à la valeur propre de valeur absolue
maximum. Pour des distributions de contacts initialement
non-aléatoires ou pour des histoires de chargements complexes, les
deux directions majeures citées ci-dessus ne coïncident pas
a priori. Afin de tenir compte de ces situations, Oda
& al. [OO92] proposent de définir un angle 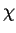 . Cet angle
est défini entre les deux directions principales majeures du
tenseur
. Cet angle
est défini entre les deux directions principales majeures du
tenseur
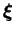 et de l'incrément de la partie
déviatoire
et de l'incrément de la partie
déviatoire
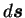 du tenseur des contraintes. Les
directions principales de
du tenseur des contraintes. Les
directions principales de
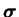 et
et
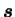 étant confondues, seule la partie déviatoire de
étant confondues, seule la partie déviatoire de
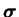 contribue à modifier les composantes du tenseur de
structure.
Finalement, ces auteurs proposent de relier l'évolution du tenseur
de structure à l'histoire de chargement imposée par une fonction
contribue à modifier les composantes du tenseur de
structure.
Finalement, ces auteurs proposent de relier l'évolution du tenseur
de structure à l'histoire de chargement imposée par une fonction
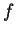 dépendante de deux arguments.
Les auteurs ne suggèrent pas de forme particulière pour la
fonction
dépendante de deux arguments.
Les auteurs ne suggèrent pas de forme particulière pour la
fonction 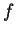 . Le terme
. Le terme
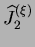 est une valeur dite
limite de
est une valeur dite
limite de
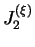 . Il s'agit d'une valeur de saturation à
l'évolution de la fonction
. Il s'agit d'une valeur de saturation à
l'évolution de la fonction
 . Cette valeur peut
être atteinte par exemple pour des états de contrainte très élevés
(compression en matrice) ou par l'apparition d'une fissure
associée à un état de cisaillement donné. L'exemple de la
fissuration suggère que les évolutions limites des distributions
de contact doivent être associées à d'autres phénomènes que la
seule action du deuxième invariant des contraintes.
En outre, des propriétés particulières de la fonction
. Cette valeur peut
être atteinte par exemple pour des états de contrainte très élevés
(compression en matrice) ou par l'apparition d'une fissure
associée à un état de cisaillement donné. L'exemple de la
fissuration suggère que les évolutions limites des distributions
de contact doivent être associées à d'autres phénomènes que la
seule action du deuxième invariant des contraintes.
En outre, des propriétés particulières de la fonction 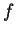 sont
proposées. Cette fonction est maximum pour
sont
proposées. Cette fonction est maximum pour
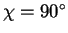 et minimum
pour
et minimum
pour 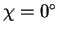 . Ceci signifie que la structure du réseau de
contact est fortement (resp. faiblement) modifiée au sens de la
valeur de l'incrément
. Ceci signifie que la structure du réseau de
contact est fortement (resp. faiblement) modifiée au sens de la
valeur de l'incrément
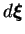 si l'orientation
majoritaire des normales de contact forme un angle de 90^&cir#circ; (resp.
de 0^&cir#circ;) par rapport à la direction de la contrainte principale
majeure. Cette fonction est également supposée croissante par
rapport à
si l'orientation
majoritaire des normales de contact forme un angle de 90^&cir#circ; (resp.
de 0^&cir#circ;) par rapport à la direction de la contrainte principale
majeure. Cette fonction est également supposée croissante par
rapport à
![$ [\sqrt{\widehat{J}_2^{(\xi)}} - \sqrt{J_2^{(\xi)}}]$](img562.png) ,
avec un minimum en
,
avec un minimum en
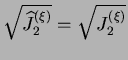 . La structure du réseau des contacts est
modifiée d'autant plus rapidement que la valeur du second
invariant de
. La structure du réseau des contacts est
modifiée d'autant plus rapidement que la valeur du second
invariant de
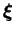 est éloignée de la valeur de
saturation associée au mode de chargement appliqué.
Suite à l'ensemble de ces considérations en rapport avec les
travaux de Oda & al. [OO92] une remarque est à souligner. À
partir de considérations en rapport avec une approche
micromécanique (
est éloignée de la valeur de
saturation associée au mode de chargement appliqué.
Suite à l'ensemble de ces considérations en rapport avec les
travaux de Oda & al. [OO92] une remarque est à souligner. À
partir de considérations en rapport avec une approche
micromécanique (
 ) ces auteurs proposent un
formalisme adapté à une approche phénoménologique permettant de
déduire l'évolution du tenseur de structure relatif à un ensemble
de grains à l'échelle macroscopique. La mise en
) ces auteurs proposent un
formalisme adapté à une approche phénoménologique permettant de
déduire l'évolution du tenseur de structure relatif à un ensemble
de grains à l'échelle macroscopique. La mise en  uvre de ce
formalisme nécessite une définition du tenseur de structure
uvre de ce
formalisme nécessite une définition du tenseur de structure
 initiale avant application du chargement.
Pour les milieux poreux, la contrainte effective prend en compte
la porosité du milieu afin de savoir quelle est la contrainte que
subit le squelette. Pour déterminer cette contrainte effective, la
surface totale de l'échantillon est diminuée de la surface des
port afin de ne prendre en compte que la surface de matière.
ainsi, la contrainte effective est le résultat du rapport entre la
force appliquée à l'ensemble de la surface et la surface de l a
matière. Cette contrainte effective est alors supérieur ou égale à
la contrainte apparente qui elle, est le rapport entre la force
appliquée et la surface totale.
Dans le cas des des milieux pulvérulents, qui sont une sous classe
des milieux poreux, il y a en plus une notion d'orientation de la
surface de contact. Ainsi, il est possible de définir une surface
effective de contact orientée par :
initiale avant application du chargement.
Pour les milieux poreux, la contrainte effective prend en compte
la porosité du milieu afin de savoir quelle est la contrainte que
subit le squelette. Pour déterminer cette contrainte effective, la
surface totale de l'échantillon est diminuée de la surface des
port afin de ne prendre en compte que la surface de matière.
ainsi, la contrainte effective est le résultat du rapport entre la
force appliquée à l'ensemble de la surface et la surface de l a
matière. Cette contrainte effective est alors supérieur ou égale à
la contrainte apparente qui elle, est le rapport entre la force
appliquée et la surface totale.
Dans le cas des des milieux pulvérulents, qui sont une sous classe
des milieux poreux, il y a en plus une notion d'orientation de la
surface de contact. Ainsi, il est possible de définir une surface
effective de contact orientée par :
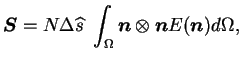 |
(4.29.4) |
où 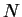 est le nombre total de contacts dans la section considérée
dont la surface moyenne est
est le nombre total de contacts dans la section considérée
dont la surface moyenne est
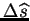 et
et
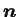 est le vecteur normal à la section observée. C'est alors à
cette surface orientée que sera rapporté l'effort pour déterminer
la contrainte effective. Par ailleurs, on identifie le tenseur de
structure
est le vecteur normal à la section observée. C'est alors à
cette surface orientée que sera rapporté l'effort pour déterminer
la contrainte effective. Par ailleurs, on identifie le tenseur de
structure
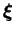 dans l'équation (4.5.4).
Or, il n'est pas ici souhaité de prendre en compte la contrainte
subit par le squelette, mais seulement prendre en compte
l'orientation des contacts. Ainsi, le tenseur de structure des
normales de contact
dans l'équation (4.5.4).
Or, il n'est pas ici souhaité de prendre en compte la contrainte
subit par le squelette, mais seulement prendre en compte
l'orientation des contacts. Ainsi, le tenseur de structure des
normales de contact
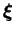 est utilisé pour définir un
tenseur des contraintes modifiées noté
est utilisé pour définir un
tenseur des contraintes modifiées noté
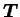 tenant
compte de ces orientations de contacts. La définition de ce
nouveau tenseur est donnée par l'équation (4.5.5).
tenant
compte de ces orientations de contacts. La définition de ce
nouveau tenseur est donnée par l'équation (4.5.5).
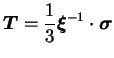 |
(4.29.5) |
Le produit du tenseur de structure avec le tenseur des contraintes
de Cauchy implique que la spécificité de la structure du matériau
est prise en compte. Ainsi, le tenseur des contraintes modifiées
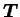 prend en considération la propriété d'anisotropie
du matériau.
Ce tenseur des contraintes modifiées
prend en considération la propriété d'anisotropie
du matériau.
Ce tenseur des contraintes modifiées
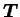 n'est pas
symétrique (
n'est pas
symétrique (
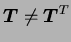 ). En effet :
Cette propriété implique qu'il n'est pas possible d'avoir les
mêmes pratiques avec ce tenseur
). En effet :
Cette propriété implique qu'il n'est pas possible d'avoir les
mêmes pratiques avec ce tenseur
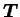 qu'avec le tenseur
des contraintes de Cauchy
qu'avec le tenseur
des contraintes de Cauchy
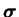 . La démarche
proposée pour la détermination de surface de charges relative à un
comportement anisotrope consiste à utiliser les invariants de
. La démarche
proposée pour la détermination de surface de charges relative à un
comportement anisotrope consiste à utiliser les invariants de
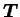 . En particulier, une surface de charges décrite
avec les invariants de
. En particulier, une surface de charges décrite
avec les invariants de
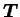 sous la forme d'un critère
isotrope se traduit par un critère de forme anisotrope avec des
invariants du tenseur
sous la forme d'un critère
isotrope se traduit par un critère de forme anisotrope avec des
invariants du tenseur
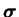 . Le point d'intérêt à
relever consiste finalement en l'utilisation d'une transformation
du tenseur de Cauchy pour formaliser l'équation d'une surface de
charge sur la base des invariants de
. Le point d'intérêt à
relever consiste finalement en l'utilisation d'une transformation
du tenseur de Cauchy pour formaliser l'équation d'une surface de
charge sur la base des invariants de
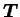 .
Ainsi, il est possible de transformer une surface de charges
isotrope en une surface de charges anisotrope en remplaçant les
invariants de
.
Ainsi, il est possible de transformer une surface de charges
isotrope en une surface de charges anisotrope en remplaçant les
invariants de
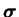 par ceux de
par ceux de
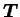 .
Afin de visualiser cette transformation de l'espace des
contraintes et de définir des relations entre les invariants de
chacun des tenseurs, il faut considérer des espaces vectoriels
dont les bases sont les invariants des tenseurs
.
Afin de visualiser cette transformation de l'espace des
contraintes et de définir des relations entre les invariants de
chacun des tenseurs, il faut considérer des espaces vectoriels
dont les bases sont les invariants des tenseurs
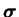 et
et
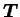 . En se limitant aux deux premiers
invariants, il vient :
. En se limitant aux deux premiers
invariants, il vient :
| espace vectoriel |
|
espace vectoriel |
des invariants de
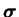 |
|
des invariants de
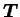 |
 |
 |
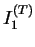 |
 |
|
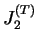 |
Il existe des relations et leurs réciproques entre ces deux
espaces vectoriels :
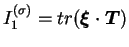 |
(4.29.6) |
![$\displaystyle J_2^{(\sigma)} = \frac{1}{2}\left[ tr \left( \left( \boldsymbol
...
... - \frac{1}{3} tr^2
\left( \boldsymbol \xi \cdot \boldsymbol T \right) \right]$](img576.png) |
(4.29.7) |
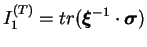 |
(4.29.8) |
![$\displaystyle J_2^{(T)} = \frac{1}{2}\left[ tr \left( \left( \boldsymbol \xi
^...
...{3}
tr^2 \left( \boldsymbol \xi^{-1} \cdot \boldsymbol \sigma \right)
\right]$](img578.png) |
(4.29.9) |
Le tenseur de structure
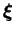 présent dans ces
relations souligne la prise en compte des distributions des
normales de contact dans le comportement plastique. Les deux
dernières relations indiquent en particulier que pour une surface
de charge isotrope exprimée avec les invariants de
présent dans ces
relations souligne la prise en compte des distributions des
normales de contact dans le comportement plastique. Les deux
dernières relations indiquent en particulier que pour une surface
de charge isotrope exprimée avec les invariants de
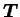 , sa traduction en contraintes
, sa traduction en contraintes
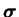 fait
intervenir deux invariants supplémentaires aux trois invariants
initiaux de l'espace des contraintes de Cauchy. Dans le cas
général, on obtient :
fait
intervenir deux invariants supplémentaires aux trois invariants
initiaux de l'espace des contraintes de Cauchy. Dans le cas
général, on obtient :
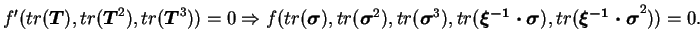 |
(4.29.10) |
Une telle expression de la surface de charges en fonction de la
contrainte
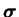 correspond à la théorie générale
des représentations des surfaces de charges développées par
Boehler & al. [BOE97] (dans son chapitre 5).
Par ailleurs, l'expression du tenseur des contraintes modifiées
donnée par l'équation (4.5.5) est une opération équivalente à
la transformation proposée par la théorie simplifiée de Boehler
dans l'équation (4.5.1). La différence se situe au
niveau de l'ordre du tenseur d'anisotropie. Par contre le but de
ces deux traitements formels est commun, il s'agit de pouvoir
utiliser les critères de plasticité isotropes afin de les
transformer en critères anisotropes. Ceci est illustré par la
figure 4.5.3.
correspond à la théorie générale
des représentations des surfaces de charges développées par
Boehler & al. [BOE97] (dans son chapitre 5).
Par ailleurs, l'expression du tenseur des contraintes modifiées
donnée par l'équation (4.5.5) est une opération équivalente à
la transformation proposée par la théorie simplifiée de Boehler
dans l'équation (4.5.1). La différence se situe au
niveau de l'ordre du tenseur d'anisotropie. Par contre le but de
ces deux traitements formels est commun, il s'agit de pouvoir
utiliser les critères de plasticité isotropes afin de les
transformer en critères anisotropes. Ceci est illustré par la
figure 4.5.3.
Figure 4.5.3:
Transformation de l'espace des contraintes afin d'exprimer
le critère de plasticité sous une forme isotrope
|
|
Les auteurs Oda & al. [OO92] ont ainsi utilisé ce
formalisme pour transformer le modèle modifié non-cohésif de
CamClay isotrope en un modèle anisotrope. Le modèle de CamClay
isotrope considéré est donné par l'équation (4.5.11).
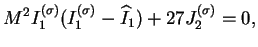 |
(4.29.11) |
où
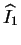 est le paramètre d'écrouissage qui dépend
uniquement de la déformation volumique plastique
(
est le paramètre d'écrouissage qui dépend
uniquement de la déformation volumique plastique
(
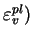 . Ce paramètre peut être identifié à
. Ce paramètre peut être identifié à 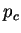 dans l'équation (4.4.1).
Le remplacement de
dans l'équation (4.4.1).
Le remplacement de
 et
et
 par les
invariants du tenseur des contraintes modifiées,
par les
invariants du tenseur des contraintes modifiées, 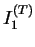 et
et
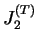 , donne la nouvelle surface de charges qui a pour
expression (4.5.12).
, donne la nouvelle surface de charges qui a pour
expression (4.5.12).
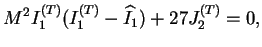 |
(4.29.12) |
où
 et
et
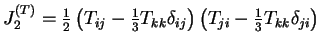 (car
(car 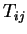 n'est pas symétrique).
L'équation (4.5.12) peut être réécrite en introduisant les
équations (4.5.8) et (4.5.9) afin d'exprimer la surface de
charge dans l'espace des contraintes de Cauchy :
n'est pas symétrique).
L'équation (4.5.12) peut être réécrite en introduisant les
équations (4.5.8) et (4.5.9) afin d'exprimer la surface de
charge dans l'espace des contraintes de Cauchy :
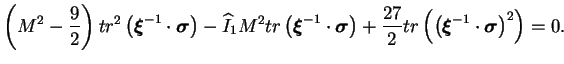 |
(4.29.13) |
Il est à noter que le passage de l'équation (4.5.12) à
l'équation (4.5.13) est traduit par
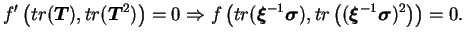 |
(4.29.14) |
Les composantes de l'expression (4.5.14) appartiennent à
la base des composantes de l'expression (4.5.10). Cela implique
que la transformation de l'espace des contraintes proposée par Oda
& al. [OO92] est incluse dans la théorie générale des
représentations des surfaces de charges développée par Boehler
& al. [BOE97].
Afin de concrétiser la représentation de cette surface de
chargess, il proposé ici une application numérique dans le cas
d'une compression triaxiale de révolution. La pente d'état
critique 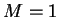 , le tenseur de structure
, le tenseur de structure
 est
donné par :
et la forme du tenseur des contraintes est :
Ainsi, l'application numérique de l'équation (4.5.13)
s'écrit :
est
donné par :
et la forme du tenseur des contraintes est :
Ainsi, l'application numérique de l'équation (4.5.13)
s'écrit :
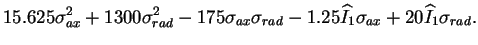 |
(4.29.15) |
Dans ces conditions, la pression isotrope et la contrainte
équivalente de Von Mises ont respectivement pour expressions :
et
Il est donc possible d'exprimer l'équation (4.5.15) en fonction de 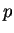 et
et 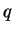 . Dans le cas où
. Dans le cas où
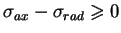 , on a :
Cette équation décrit une ellipse dans un plan
, on a :
Cette équation décrit une ellipse dans un plan 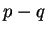 dont le grand
axe n'est pas parallèle à l'axe
dont le grand
axe n'est pas parallèle à l'axe 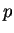 .
Le résultat de cette transformation a été confronté aux mesures
expérimentales de Yasufuku [YAS90]. La prospection de
l'espace des contraintes
.
Le résultat de cette transformation a été confronté aux mesures
expérimentales de Yasufuku [YAS90]. La prospection de
l'espace des contraintes 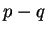 présentée sur la figure 4.5.4
utilise huit échantillons pré-consolidés jusqu'au point A puis
déchargés jusqu'au point B. À partir de ce point, huit chemins de
contrainte ont été testés afin de déterminer la surface de
charges. Il a été procédé de la même façon pour les mesures de la
figure 4.5.5. Dans le cas des graphiques présentés sur ces
deux figures, l'axe "q" est défini comme la différence entre la
contrainte axiale et la contrainte radiale
(
présentée sur la figure 4.5.4
utilise huit échantillons pré-consolidés jusqu'au point A puis
déchargés jusqu'au point B. À partir de ce point, huit chemins de
contrainte ont été testés afin de déterminer la surface de
charges. Il a été procédé de la même façon pour les mesures de la
figure 4.5.5. Dans le cas des graphiques présentés sur ces
deux figures, l'axe "q" est défini comme la différence entre la
contrainte axiale et la contrainte radiale
(
 ). Ceci explique les valeurs
négatives prises par "q".
). Ceci explique les valeurs
négatives prises par "q".
Figure 4.5.4:
Surface de charge pour une consolidation isotrope
|
|
Figure 4.5.5:
Surface de charge pour une consolidation anisotrope
|
|
Il est à noter que la surface de charges décrite par la figure
4.5.5 est semblable aux surfaces de la figure
2.6.7. Cette similitude est fondée sur l'effet de
l'histoire de chargement. Pour la figure 2.6.7,
l'histoire de mise en forme de l'échantillon fait intervenir une
composante déviatoire en plus de la composante isotrope de la
contrainte. Cette histoire de chargement particulière est
similaire aux sollicitations appliquées à l'échantillon dont le
comportement est défini à la figure 4.5.5.
La figure 4.5.6 représente la surface de charges pour
différentes orientations de l'axe majeur principal des contraintes
appliquées par rapport à celles du tenseur 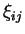 .
.
Figure 4.5.6:
Surface de charge pour une consolidation anisotrope
|
|
Il est possible de noter une similitude de la surface
d'orientation à 90^&cir#circ; de la figure 4.5.6 par rapport à la
surface de charges du modèle de CamClay initial présenté sur la
figure 4.4.1 ou encore, par rapport aux surfaces de charge
de la figure 2.6.6. On note également la
ressemblance entre la surface orientée à 60^&cir#circ; de cette figure
4.5.6 et la surface de CamClay modifiée non-cohésif de la
figure 4.4.2. Le modèle initial et le
modèle modifié peuvent être ainsi synthétisés par le seul modèle
de CamClay anisotrope. De plus, il semble que cette théorie
permette une modélisation du comportement plastique des poudres de
fer ainsi que le suggère les comparaisons entre les surfaces de
charges décrites par cette théorie et les mesures expérimentales
de Rottmann & al. [RCR01].




suivant: Homothétie isotrope, translation cinétique
monter: Théorie plastique pour les
précédent: Théorie plastique pour les
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[width=133mm]{contactparticule.eps}](img534.png)
![\includegraphics[width=133mm]{contactparticule.eps}](img534.png)
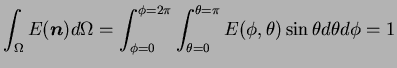
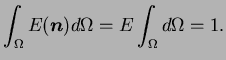
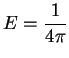
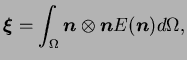
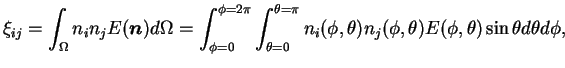
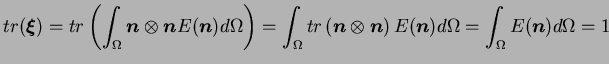
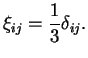
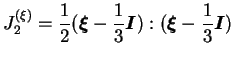
![\includegraphics[height=9cm]{evolaniso.eps}](img181.png)
![$\displaystyle d\boldsymbol \xi = f\left[\chi,
\sqrt{\widehat{J}_2^{(\xi)}}-\sqrt{J_2^{(\xi)}}\right]
d\boldsymbol s
$](img557.png)
![$ [\sqrt{\widehat{J}_2^{(\xi)}} - \sqrt{J_2^{(\xi)}}]$](img562.png) ,
avec un minimum en
,
avec un minimum en
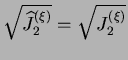 . La structure du réseau des contacts est
modifiée d'autant plus rapidement que la valeur du second
invariant de
. La structure du réseau des contacts est
modifiée d'autant plus rapidement que la valeur du second
invariant de
![\includegraphics[]{transformationOda.eps}](img580.png)