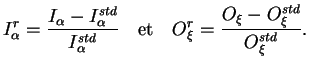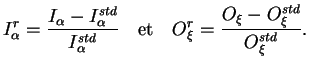suivant: Étude de sensibilité pour
monter: Étude de sensibilité
précédent: La pression isotrope de
Table des matières
Définition du critère de sensibilité
Les perturbations appliquées aux évolutions de référence de la loi
de comportement Drucker-Prager/Cap constituent autant de fichiers
d'entrées différents pour les simulations numériques. A titre
d'illustration, l'étude de sensibilité pour un paramètre conduit à
produire quatre simulations afin de mener l'étude au sens du
principe exposé par la figure 7.2.1. Le nombre total
de simulations à produire est donc de 24, les résultats numériques
associés au cas de référence de la pièce E étant déjà acquis. Les
résultats numériques analysés correspondent à la fin de la
compression. Ils concernent plus particulièrement les densités
moyennes dans les zones 1 à 5 et les efforts maximaux sur les
trois poinçons.
Compte tenu du grand nombre de valeurs à considérer, un critère
associé à la sensibilité est établi afin de rendre plus
synthétique les conclusions de cette étude. Le calcul de ce
critère nécessite au préalable des définitions particulières pour
les entrées (variations imposées) et les sorties (résultats
numériques).
Les entrées sont au sens de la simulation numérique constituées
par des fonctions de la déformation volumique plastique. Ces
différentes fonctions sont distinguées de manière simple par des
valeurs scalaires, notées 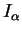 pour les variations et
pour les variations et
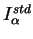 pour la référence. Ces valeurs scalaires
caractérisent chaque fonction par sa valeur initiale ou sa valeur
finale comme cela est illustré par la figure 7.2.1.
L'indice
pour la référence. Ces valeurs scalaires
caractérisent chaque fonction par sa valeur initiale ou sa valeur
finale comme cela est illustré par la figure 7.2.1.
L'indice 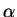 correspond alternativement au nom d'un des six
paramètres de la loi de comportement de la poudre. La différence
entre les termes
correspond alternativement au nom d'un des six
paramètres de la loi de comportement de la poudre. La différence
entre les termes 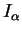 et
et
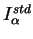 est déterminée par
l'incertitude expérimentale envisagée pour chacun des paramètres.
Chaque valeur de sortie est égalée à l'une des quantités simulées,
c'est à dire une des densités moyennes dans les zones 1 à 5 ou
l'un des trois efforts maximaux sur les poinçons. Les sorties sont
notées
est déterminée par
l'incertitude expérimentale envisagée pour chacun des paramètres.
Chaque valeur de sortie est égalée à l'une des quantités simulées,
c'est à dire une des densités moyennes dans les zones 1 à 5 ou
l'un des trois efforts maximaux sur les poinçons. Les sorties sont
notées  pour des résultats numériques associés à une
perturbation et
pour des résultats numériques associés à une
perturbation et
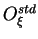 pour les résultats de référence.
L'indice
pour les résultats de référence.
L'indice 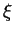 prend alternativement le nom d'une des huit
quantités considérées comme sorties. La différence entre les
termes
prend alternativement le nom d'une des huit
quantités considérées comme sorties. La différence entre les
termes  et
et
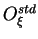 traduit l'influence des variations
d'entrées sur les résultats numérique de la simulation.
À partir de ces définitions des entrées et des sorties, il est
possible de calculer la variation relative imposée aux entrées et
la variation relative consécutive à la simulation sur les sorties.
Les variations relatives des sorties
traduit l'influence des variations
d'entrées sur les résultats numérique de la simulation.
À partir de ces définitions des entrées et des sorties, il est
possible de calculer la variation relative imposée aux entrées et
la variation relative consécutive à la simulation sur les sorties.
Les variations relatives des sorties 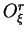 sont a
priori reliées aux variations relatives des paramètres d'entrée
de la loi
sont a
priori reliées aux variations relatives des paramètres d'entrée
de la loi
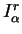 . Cette dépendance est quantitativement
exprimée au travers du critère de sensibilité. Dans le cadre de
cette étude paramétrique, le critère de sensibilité est un
scalaire déterminé par l'expression :
. Cette dépendance est quantitativement
exprimée au travers du critère de sensibilité. Dans le cadre de
cette étude paramétrique, le critère de sensibilité est un
scalaire déterminé par l'expression :
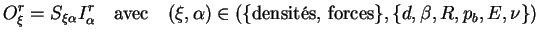 |
(7.46.1) |
Pour chaque variation relative imposée
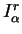 , les résultats
de simulation permettent suite à l'extraction des valeurs le
calcul du terme
, les résultats
de simulation permettent suite à l'extraction des valeurs le
calcul du terme 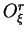 . La relation (7.4.1) est
ensuite utilisée pour l'ensemble des combinaisons (
. La relation (7.4.1) est
ensuite utilisée pour l'ensemble des combinaisons (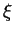 ,
,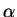 )
requises par cette étude.
Le paramètre de sensibilité
)
requises par cette étude.
Le paramètre de sensibilité
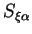 prend la forme d'un
scalaire reliant les valeurs
prend la forme d'un
scalaire reliant les valeurs 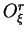 et
et
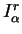 de façon
proportionnelle. Cette apparente linéarité entre les termes
de façon
proportionnelle. Cette apparente linéarité entre les termes
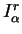 et
et 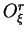 ne peut pas être avérée sans une étude
particulière. Il demeure en effet possible que le critère de
sensibilité
ne peut pas être avérée sans une étude
particulière. Il demeure en effet possible que le critère de
sensibilité
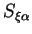 soit une fonction non constante
dépendante du terme
soit une fonction non constante
dépendante du terme
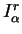 . Le nombre des simulations
numériques par éléments finis n'est pas suffisant pour analyser
correctement cette dépendance éventuelle de
. Le nombre des simulations
numériques par éléments finis n'est pas suffisant pour analyser
correctement cette dépendance éventuelle de
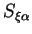 en
fonction de
en
fonction de
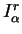 . Une étude d'un cas simplifié est
proposée afin d'éclaircir ce point. Cette étude serait également
intéressante dans un autre contexte car elle fournit des
indicateurs utiles pour le traitement des données expérimentales
issues d'une compression en matrice.
. Une étude d'un cas simplifié est
proposée afin d'éclaircir ce point. Cette étude serait également
intéressante dans un autre contexte car elle fournit des
indicateurs utiles pour le traitement des données expérimentales
issues d'une compression en matrice.




suivant: Étude de sensibilité pour
monter: Étude de sensibilité
précédent: La pression isotrope de
Table des matières
FRACHON Arnaud
2002-11-12