



suivant: Résultats pour la pièce
monter: Étude de sensibilité
précédent: Définition du critère de
Table des matières
Le cas simplifié proposé consiste en l'étude de la compression en
matrice d'un cylindre en supposant qu'il n'y a pas de frottement
entre la poudre et l'outillage. Ce cas simplifié a pour avantage
majeur de pouvoir être résolu littéralement. En effet, les
hypothèses de compression sans frottement et de forme cylindrique
pour la pièce permettent de considérer des états de déformation et
de contrainte homogènes. Une dernière hypothèse simplificatrice
consiste à supposer un comportement purement plastique, seules les
évolutions des paramètres de la surface de charges sont
considérées dans les calculs. Cette première étude de sensibilité
concerne alors les quatre paramètres (d,  , R,
, R,  ) du
modèle de Drucker-Prager/Cap.
Les conditions aux limites cinématiques induisent des déformations
radiales nulles. Il vient alors que
) du
modèle de Drucker-Prager/Cap.
Les conditions aux limites cinématiques induisent des déformations
radiales nulles. Il vient alors que
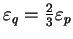 , avec
, avec
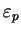 la déformation volumique et
la déformation volumique et
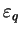 la déformation équivalente déviatoire. La
direction de l'écoulement plastique associée aux déformations est
normale à la surface de charges. L'état de contrainte au cours de
la compression est alors déduit par le lieu des points dont la
normale à la surface de charges est de pente
la déformation équivalente déviatoire. La
direction de l'écoulement plastique associée aux déformations est
normale à la surface de charges. L'état de contrainte au cours de
la compression est alors déduit par le lieu des points dont la
normale à la surface de charges est de pente
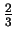 .
Dans le cas du modèle de Drucker-Prager/Cap (voir paragraphe
4.4.2 en page
.
Dans le cas du modèle de Drucker-Prager/Cap (voir paragraphe
4.4.2 en page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), l'état de
contraintes correspondant à ce lieu de point est calculé à partir
des équations (7.5.1) et (7.5.2).
), l'état de
contraintes correspondant à ce lieu de point est calculé à partir
des équations (7.5.1) et (7.5.2).
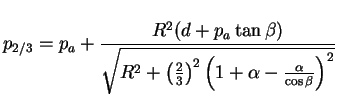 |
(7.47.1) |
 |
(7.47.2) |
Les paramètres (d,  , R,
, R, 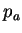 ) sont des fonctions de la
déformation volumique plastique homogène dans toute la pièce.
L'état de contrainte peut ainsi être paramétré par l'évolution de
la déformation volumique plastique.
Une étude de sensibilité sur les répartitions de densité n'a ici
aucun sens puisque la déformation est homogène. Ce cas simplifié
est traité de la même façon que les modèles de simulation car la
cinématique du poinçon de compression est considérée comme une
donnée d'entrée. La déformation homogène et la densité courante
sont ainsi entièrement déterminées par la cinématique.
La sensibilité de la valeur de l'effort de compression par rapport
aux variations appliquées aux paramètres de la loi plastique peut
être étudiée analytiquement. Les efforts axiaux et radiaux au sein
de la matrice sont reliés aux contraintes par l'intermédiaire des
surfaces sur lesquelles elles sont appliquées. Pour accéder à
l'expression de la force de compression, il convient de relier les
contraintes (axiale et radiale) aux quantités
) sont des fonctions de la
déformation volumique plastique homogène dans toute la pièce.
L'état de contrainte peut ainsi être paramétré par l'évolution de
la déformation volumique plastique.
Une étude de sensibilité sur les répartitions de densité n'a ici
aucun sens puisque la déformation est homogène. Ce cas simplifié
est traité de la même façon que les modèles de simulation car la
cinématique du poinçon de compression est considérée comme une
donnée d'entrée. La déformation homogène et la densité courante
sont ainsi entièrement déterminées par la cinématique.
La sensibilité de la valeur de l'effort de compression par rapport
aux variations appliquées aux paramètres de la loi plastique peut
être étudiée analytiquement. Les efforts axiaux et radiaux au sein
de la matrice sont reliés aux contraintes par l'intermédiaire des
surfaces sur lesquelles elles sont appliquées. Pour accéder à
l'expression de la force de compression, il convient de relier les
contraintes (axiale et radiale) aux quantités 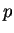 et
et 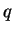 .
.
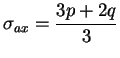 |
(7.47.3) |
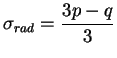 |
(7.47.4) |
L'effort de compression est proportionnel à la contrainte axiale.
La densité et la contrainte axiale sont homogènes pour ce cas
simplifié, l'effort de compression s'obtient directement par
multiplication de la surface de contact avec le poinçon et de la
contrainte axiale. A cet égard, l'étude de sensibilité est
directement menée sur le terme de contrainte axiale.
Afin de simplifier les expressions, le coefficient 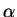 est
supposé nul. Le coefficient
est
supposé nul. Le coefficient 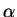 conditionne la géométrie de
la surface de transition, cette simplification n'a pas de
conséquence sur les résultats de sensibilité pour le cas de
compression étudié. La contrainte axiale a ainsi pour expression
:
conditionne la géométrie de
la surface de transition, cette simplification n'a pas de
conséquence sur les résultats de sensibilité pour le cas de
compression étudié. La contrainte axiale a ainsi pour expression
:
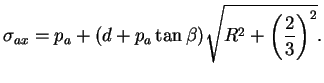 |
(7.47.5) |
Dans le cadre de cette étude analytique, il est possible de
décrire la sensibilité par rapport aux paramètres plastiques de façon continue
en fonction de la déformation volumique plastique. La relation
(7.4.1) s'exprime comme (7.5.6) pour le cas
simplifié.
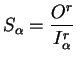 |
(7.47.6) |
Le terme 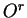 correspond à la variation relative de la contrainte
axiale
correspond à la variation relative de la contrainte
axiale
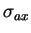 . L'indice
. L'indice 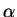 prend alternativement le
nom d'une des quatre quantités (d,
prend alternativement le
nom d'une des quatre quantités (d,  , R,
, R, 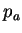 ). Si le terme
(
). Si le terme
(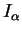 -
-
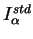 ) tend vers zéro, l'expression de la
sensibilité prend la forme particulière suivante :
) tend vers zéro, l'expression de la
sensibilité prend la forme particulière suivante :
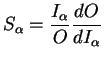 |
(7.47.7) |
L'équation (7.5.7) traduit ainsi la sensibilité comme
une fonction proportionnelle à la dérivée de la sortie par rapport
à l'entrée. Cette équation conduit à calculer les dérivées
partielles de la contrainte axiale
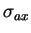 par rapport à
chacune des entrées
par rapport à
chacune des entrées 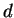 ,
,  ,
, 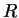 et
et  .
.
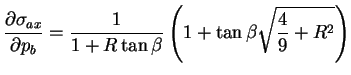 |
(7.47.8) |
 |
(7.47.9) |
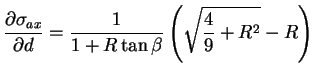 |
(7.47.10) |
 |
(7.47.11) |
L'équation (7.5.7) permet d'observer l'évolution de la
sensibilité de la contrainte
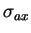 tout au long de la
compression puisque les dérivées exprimées par les expressions
(7.5.8), (7.5.9), (7.5.10) et (7.5.11) sont
littérales. En outre, on remarque que l'expression de la
sensibilité dans l'équation (7.5.7) correspond au poids
de la contribution de l'erreur relative d'un paramètre
tout au long de la
compression puisque les dérivées exprimées par les expressions
(7.5.8), (7.5.9), (7.5.10) et (7.5.11) sont
littérales. En outre, on remarque que l'expression de la
sensibilité dans l'équation (7.5.7) correspond au poids
de la contribution de l'erreur relative d'un paramètre 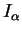 exprimé par Zavaliangos [ZAV97]. D'après cette définition, la
sensibilité peut être interprétée ici comme l'importance de
l'influence d'un paramètre sur le résultat de la simulation
numérique. Cela correspond exactement en ce sens à la définition
donnée par l'équation (7.4.1).
La sensibilité de la contrainte axiale par rapport à chaque
paramètre peut être calculée en introduisant dans l'expression de
exprimé par Zavaliangos [ZAV97]. D'après cette définition, la
sensibilité peut être interprétée ici comme l'importance de
l'influence d'un paramètre sur le résultat de la simulation
numérique. Cela correspond exactement en ce sens à la définition
donnée par l'équation (7.4.1).
La sensibilité de la contrainte axiale par rapport à chaque
paramètre peut être calculée en introduisant dans l'expression de
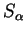 la dérivée partielle correspondante. Les évolutions
numériques particulières des paramètres
la dérivée partielle correspondante. Les évolutions
numériques particulières des paramètres 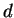 ,
,  ,
, 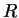 ,
,  sont utilisées, les quatre fonctions de sensibilités associées
sont présentées sur la figure 7.5.1.
sont utilisées, les quatre fonctions de sensibilités associées
sont présentées sur la figure 7.5.1.
Figure 7.5.1:
Évolutions de la sensibilité de la contrainte de
compression par rapport aux paramètres plastiques au cours de la
compression
|
|
Ceci indique que les paramètres  ,
, 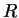 et
et  ont une
influence sur la contrainte axiale bien supérieure à celle du
paramètre
ont une
influence sur la contrainte axiale bien supérieure à celle du
paramètre 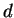 . Afin de connaître les sensibilités en début de
compression, il suffit de relever les valeurs de
. Afin de connaître les sensibilités en début de
compression, il suffit de relever les valeurs de 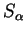 pour
une déformation volumique plastique nulle. Le paramètre
pour
une déformation volumique plastique nulle. Le paramètre  a
une influence fortement décroissante sur la sensibilité entre le
début et la fin de la compression. La valeur de la contrainte
axiale
a
une influence fortement décroissante sur la sensibilité entre le
début et la fin de la compression. La valeur de la contrainte
axiale
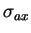 est dépendante au cours de la compression du
chemin de contrainte suivi dans le plan P-Q. La figure
7.5.1 indique que le chemin de contrainte le moins
perturbé devrait être celui associé aux variations numériques
imposées à d. La perturbation maximum du chemin devrait être
obtenue par les variations imposées au paramètre
est dépendante au cours de la compression du
chemin de contrainte suivi dans le plan P-Q. La figure
7.5.1 indique que le chemin de contrainte le moins
perturbé devrait être celui associé aux variations numériques
imposées à d. La perturbation maximum du chemin devrait être
obtenue par les variations imposées au paramètre  . Les
sensibilités aux paramètres
. Les
sensibilités aux paramètres 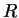 et
et  sont significativement
variables en fonction de la déformation volumique plastique. La
figure 7.5.2 illustre l'influence des variations
numériques proposées pour les fortes déformations plastiques sur
le chemin de contrainte caractéristique de la compression en
matrice.
sont significativement
variables en fonction de la déformation volumique plastique. La
figure 7.5.2 illustre l'influence des variations
numériques proposées pour les fortes déformations plastiques sur
le chemin de contrainte caractéristique de la compression en
matrice.
Figure 7.5.2:
Chemins de contraintes dans des plans p-q pour une
variation imposée en fin de compression à chaque paramètre
plastique
|
|
Il est alors possible de conclure que les valeurs du critère de
sensibilité traduit fidèlement l'influence croissante des
paramètres 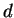 ,
,  ,
, 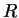 et
et  sur les chemins de
contrainte. Cette figure permet l'illustration de l'équation de la
surface de charges (4.4.7) (page
sur les chemins de
contrainte. Cette figure permet l'illustration de l'équation de la
surface de charges (4.4.7) (page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) pour
laquelle les coefficients
) pour
laquelle les coefficients 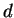 et
et  n'interviennent que dans
la position du centre du cap. La forme et la position de cette
surface sont essentiellement décrites par les paramètres
n'interviennent que dans
la position du centre du cap. La forme et la position de cette
surface sont essentiellement décrites par les paramètres 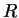 et
et
 . Pour cette raison, les variations de ces deux derniers
paramètres modifient fortement les états de contraintes en fin de
compression. La conséquence est une grande modification de la
contrainte de compression nécessaire à la densification de la
poudre.
La figure 7.5.1 présente des résultats de l'évolution de
la sensibilité pour une définition particulière qui intègre les
dérivées partielles de
. Pour cette raison, les variations de ces deux derniers
paramètres modifient fortement les états de contraintes en fin de
compression. La conséquence est une grande modification de la
contrainte de compression nécessaire à la densification de la
poudre.
La figure 7.5.1 présente des résultats de l'évolution de
la sensibilité pour une définition particulière qui intègre les
dérivées partielles de
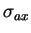 par rapport aux paramètres
par rapport aux paramètres
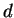 ,
,  ,
, 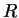 et
et  . Pour une mise en
. Pour une mise en  uvre directe de
la définition proposée à la section 7.4 (relation
7.5.6), les variations des paramètres telles qu'elles
ont été présentées en début de chapitre sont utilisées pour tracer
les évolutions de la figure 7.5.3.
uvre directe de
la définition proposée à la section 7.4 (relation
7.5.6), les variations des paramètres telles qu'elles
ont été présentées en début de chapitre sont utilisées pour tracer
les évolutions de la figure 7.5.3.
Figure 7.5.3:
Sensibilité de la contrainte au cours de la compression
par rapport aux variations des paramètres plastiques présentées en
début de chapitre
|
|
Il apparaît que ces évolutions sont très semblables à celles
présentées par la figure 7.5.1. Certaines sont légèrement
inférieures en valeur absolue ce qui signifie que le terme
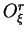 de la relation (7.4.1) est en toute rigueur
variable avec les amplitudes imposées au terme
de la relation (7.4.1) est en toute rigueur
variable avec les amplitudes imposées au terme
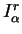 . Dans
le cadre particulier à ce chapitre, les variations
. Dans
le cadre particulier à ce chapitre, les variations
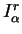 sont bornées par les incertitudes expérimentales estimées.
La sensibilité à chaque paramètre peut être décrite par un doublet
de valeurs qui correspond à des déformations volumiques plastiques
respectivement nulles et maximums. La figure 7.5.4
fournit les sensibilités de chaque paramètre pour les deux valeurs
extrêmes de la déformation.
sont bornées par les incertitudes expérimentales estimées.
La sensibilité à chaque paramètre peut être décrite par un doublet
de valeurs qui correspond à des déformations volumiques plastiques
respectivement nulles et maximums. La figure 7.5.4
fournit les sensibilités de chaque paramètre pour les deux valeurs
extrêmes de la déformation.
Figure 7.5.4:
Sensibilité de la contrainte axiale en début et en fin de
compression par rapport aux variations numériques imposées aux
paramètres plastiques
|
|
Les sensibilités sont globalement maximums en début de
compression. Ceci concerne particulièrement l'angle de frottement
interne  et l'excentricité
et l'excentricité 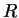 . L'état de contrainte est
plus déviatoire que sphérique (voir figure 7.5.2) en
début de compression. Le point caractéristique de l'état de
contrainte (lieu de la normale de pente 2/3) est proche de la
transition entre la surface du Cap et la droite de rupture. La
"géométrie" de cette zone de la surface de charges de
Drucker-Prager/Cap est ainsi fortement influencée par l'angle de
la droite de rupture
. L'état de contrainte est
plus déviatoire que sphérique (voir figure 7.5.2) en
début de compression. Le point caractéristique de l'état de
contrainte (lieu de la normale de pente 2/3) est proche de la
transition entre la surface du Cap et la droite de rupture. La
"géométrie" de cette zone de la surface de charges de
Drucker-Prager/Cap est ainsi fortement influencée par l'angle de
la droite de rupture  et par l'excentricité
et par l'excentricité 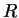 . Cette
influence de
. Cette
influence de  en début de compression ne représente pas une
généralité, elle est due à la forme numérique adoptée pour décrire
la loi de comportement aux très faibles densités. Ce commentaire
souligne que le paramètre
en début de compression ne représente pas une
généralité, elle est due à la forme numérique adoptée pour décrire
la loi de comportement aux très faibles densités. Ce commentaire
souligne que le paramètre  caractéristique du mécanisme de
Drucker-Prager a une influence sur le mécanisme activé de
densification lié au Cap. Ce point qui pourrait paraître singulier
est cependant logique. Lorsqu'une variation arbitraire est
appliquée à un paramètre, certains autres paramètres de la loi de
comportement peuvent être légèrement modifiés. Ce point est induit
par la nécessité d'obtenir, pour chaque variation de paramètre,
une surface de charges de Drucker-Prager/Cap fermée d'allure
cohérente vis-à-vis de l'ensemble des données et des formes
numériques adoptées.
Cette étude simplifiée fournit une première estimation de la
sensibilité des résultats en effort aux variations des paramètres
d'entrée de la loi de comportement. La simulation numérique de la
mise en forme de la pièce E permet une analyse plus complète car
l'étude numérique des effets sur les répartitions de densité est
alors possible. Cette deuxième étude permet aussi de rechercher
des conclusions effectives sur l'outil de simulation pour un cas
industriel.
caractéristique du mécanisme de
Drucker-Prager a une influence sur le mécanisme activé de
densification lié au Cap. Ce point qui pourrait paraître singulier
est cependant logique. Lorsqu'une variation arbitraire est
appliquée à un paramètre, certains autres paramètres de la loi de
comportement peuvent être légèrement modifiés. Ce point est induit
par la nécessité d'obtenir, pour chaque variation de paramètre,
une surface de charges de Drucker-Prager/Cap fermée d'allure
cohérente vis-à-vis de l'ensemble des données et des formes
numériques adoptées.
Cette étude simplifiée fournit une première estimation de la
sensibilité des résultats en effort aux variations des paramètres
d'entrée de la loi de comportement. La simulation numérique de la
mise en forme de la pièce E permet une analyse plus complète car
l'étude numérique des effets sur les répartitions de densité est
alors possible. Cette deuxième étude permet aussi de rechercher
des conclusions effectives sur l'outil de simulation pour un cas
industriel.




suivant: Résultats pour la pièce
monter: Étude de sensibilité
précédent: Définition du critère de
Table des matières
FRACHON Arnaud
2002-11-12
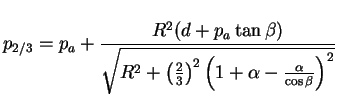
![\includegraphics[height=6cm]{senscomp.eps}](img891.png)
![\includegraphics[width=16cm]{chvarfin.eps}](img892.png)
![\includegraphics[height=6cm]{senssimple.eps}](img893.png)
![\includegraphics[height=6cm]{sensfini.eps}](img894.png)