Mesures in situ (en milieu industriel)

Dans le cadre d'une collaboration, l'entreprise Federal-Mogul a réalisé des mesures lors de la phase de compression et d'éjection d'une pièce. La poudre utilisée pour mettre en forme la pièce était une poudre de fer Distaloy AE. La pièce à vert réalisée était axisymétrique et les mesures ont été effectuées sur une presse hydraulique multi-poinçons présentée sur la figure 1.5.1. Les résultats de cette campagne d'essais ont été exposés par Kergadallan & al. [KPDP97].

Figure 1.5.1: Presse multi-poinçons

Les mesures concernent les déplacements des outils (matrice, broche, UP, LIP, LOP présentés sur la figure 1.5.1) ( mesures sur la figure 1.5.2) et les efforts exercés sur les poinçons (UP, LIP, LOP présentés sur la figure 1.5.1) (présentées sur la figure 1.5.3). Les efforts ont été mesurés par l'intermédiaire de jauges de déformations collées sur les poinçons. Après éjection, des mesures de densités ont été réalisées localement, suivant les cinq zones indiquées sur la figure 1.5.4.

Figure 1.5.2: Cinématique des outils avant pendant et après la compression

Figure: Évolution des efforts sur les poinçons durant et après la compression

Figure 1.5.4: Découpage de la pièce pour les mesures de densité

Avec ce dispositif, 5 pièces ont été formées à partir de 5 cinématiques de compression différentes. Ces cinématiques sont exposées dans le tableau 1.5.1.

Tableau 1.5.1: les différentes cinématiques pour une géométrie. Le temps est indiqué en seconde et la vitesse en mm/s. Le temps indiqué est celui pendant lequel la vitesse est appliquée à partir du début de la compression. (voir figure 1.5.2)

	Pièce A	Pièce B	Pièce C	Pièce D	Pièce E	$\Delta$
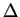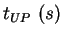$t_{UP} (s)$	1.16	1.20	1.22	1.09	1.11	10%
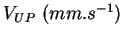$V_{UP} (mm.s^{-1})$	25.68	25.17	24.91	26.01	25.86	4.2%
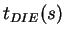$t_{DIE} (s)$	1.16	1.20	indéfinie	1.09	0.82	32%
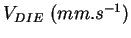$V_{DIE} (mm.s^{-1})$	13.19	13.58	indéfinie	13.66	14.66	10%
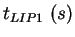$t_{LIP1} (s)$	0.43	0.52	0.22	0.25	0.39	58%
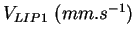$V_{LIP1} (mm.s^{-1})$	13.19	15.35	18.94	13.47	12.25	35%
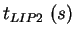$t_{LIP2} (s)$	1.03	1.05	0.97	0.85	0.96	19%
$V_{LIP2} (mm.s^{-1})$	20.18	20.46	21.03	23.02	19.44	16%

La dernière colonne du tableau 1.5.1 indique l'amplitude relative de la quantité considérée sur la ligne. Cette amplitude renseigne sur la disparité des cinématiques de façon comparable. Le premier enseignement est la faible dispersion de la cinématique du piston supérieur. Par contre, la cinématique du poinçon inférieur intérieur (LIP) est importante. La compression de la poudre qui est comprise entre le poinçon supérieur (UP) et le poinçon inférieur intérieur (LIP) est donc très variable d'une version de pièce à une autre. Par ailleurs, pour chacune de ces cinématiques, il correspond un relevé des évolutions des efforts. Celui-ci est donné dans le tableau 1.5.2.

Tableau 1.5.2: Les trois quantités $\Delta F$ correspondent aux forces à l'instant $t_{LIP1}$. Les valeurs $Fx$ sont les efforts maximums enregistrés en fin de compression. Les contre-forces appliquées lors de la phase d'éjection sont notées $\delta Fx$. L'ensemble de ces données est en relation avec la figure 1.5.3

Effort en MN	Pièce A	Pièce B	Pièce C	Pièce D	Pièce E
$\Delta F_{LIP}$	0.14	0.10	0.03	0.13	0.10
$\Delta F_{LOP}$	0.30	0.33	0.18	0.28	0.29
$\Delta F_{UP}$	0.44	0.42	0.50	0.40	0.35
$Fx_{LIP}$	1.61	1.52	1.82	2.10	1.94
$Fx_{LOP}$	0.61	0.63	0.38	0.59	0.53
$Fx_{UP}$	2.55	2.39	2.57	3.28	2.79
$\delta Fx_{LIP}$	0.03	0.01	0.10	0.10	0.09
$\delta Fx_{LOP}$	0.14	0.15	0.01	0.04	0.00
$\delta Fx_{UP}$	0.03	0.00	0.03	0.06	0.00

Il est à remarquer dans le tableau 1.5.2, les pièces B et E n'ont pas de pression supérieure pendant la phase d'éjection (les trois dernières lignes du tableau). Alors que la pièce D présente la plus grande contre-force sur le poinçon UP lors de l'éjection. Suite à l'éjection, la masse volumique a été mesurée en cinq zones. Les résultats de ces mesures sont présentés dans le tableau 1.5.3.

Tableau 1.5.3: résultats de la mesure de densité après éjection

en $g/cm^3$	Pièce A	Pièce B	Pièce C	Pièce D	Pièce E	$\Delta \rho$
zone 1	6.90	6.85	6.95	7.01	6.97	0.16
zone 2	6.93	6.90	7.01	7.07	7.02	0.17
zone 3	7.03	7.01	7.02	7.09	7.04	0.08
zone 4	6.91	6.92	6.75	6.90	6.83	0.20
zone 5	6.97	6.98	6.63	6.89	6.78	0.35
$\Delta \rho$	0.018	0.023	0.055	0.026	0.036

Dans ce tableau, la dispersion de masse volumique s'étend sur une fourchette de 18 à 55 $mg/cm^3$. Cette amplitude des dispersions est à mettre en rapport avec les observations visuelles, mais également en rapport avec les cinématiques de compression. Au regard de la dernière colonne du tableau 1.5.3, il s'avère que les dispersions de masse volumique par zone ne correspondent pas directement aux dispersions de cinématiques (ce ne sont pas les zones 1 et 2 comprises entre UP et LIP qui présentent les plus importantes dispersions). En plus des mesures quantitatives des mouvements des outillages, des efforts et des densités à vert, des observations visuelles ont été répertoriées pour qualifier l'état de la pièce après éjection. Cette méthode est souvent employée pour disqualifier des cinématiques génératrices de fissures dans la pièce par exemple. Le résultat de ces observations est présenté dans le tableau 1.5.4 qui est à conjuguer avec la figure 1.5.5.

Tableau 1.5.4: résultat des observations des pièces

Figure 1.5.5: Position des défauts sur la pièce. Ces défauts sont axisymétriques.

Seules deux de ces cinq pièces ne présentent aucun défaut apparent. Ces deux pièces correspondent aux dispersions de densités les plus faibles. De plus, la différence de densité entre la zone 3 et la zone 4 est la plus faible. Il est à noter que la plupart des défauts apparaissent lors des phases de décharge et d'éjection (80 % des causes de fissure). Les défauts peuvent être également d'ordre dimensionnel. En effet, suite à l'éjection, les dimensions radiales sont supérieures à celles de la matrice suite à l'effet du "rebond élastique" de la pièce. Dans le cas de ces pièces, les rebonds mesurés sur les diamètres sont compris entre 0.23mm et 0.33mm. Cela correspond à une déformation relative comprise entre 0.295% et 1.14%. Le rebond est non seulement fonction du matériau comprimé, mais également fonction du matériau constituant les outils. Ces déformations élastiques sont bien plus importantes que celles occasionnées lors du frittage. En effet, le retrait au frittage occasionne des variations dimensionnelles de l'ordre de 0.1% pour la poudre de fer Distaloy AE. Cette comparaison des déformations montre l'importance et l'intérêt des phases de décharge et d'éjection dans le cadre de la prédiction des dimensions de la pièce. En milieu industriel, la précision (compte tenu du rebond) est de l'ordre de 0.2% à 0.5%, mais l'objectif serait d'aboutir à une précision de 0.1%.