



suivant: Conclusion
monter: Étude de sensibilité
précédent: La pression isotrope
Table des matières
Les valeurs 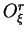 associées aux variations
associées aux variations
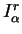 sont
présentées aux paragraphes précédents par des graphiques qui
traitent de chaque zone pour les densités et de chaque poinçon
pour les efforts. Les valeurs de sensibilité correspondent ainsi
aux pentes de chaque segment de droite.
L'ensemble de ces informations numériques est traité pour obtenir
une présentation synthétique des sensibilités pour chaque cas de
variation.
Ce traitement conduit à exposer les résultats issus des 24
simulations numériques par les quatre figures 7.7.1,
7.7.2, 7.7.3 et 7.7.4. Les valeurs
portées sur ces quatre figures correspondent à des "sensibilités
globales" qui cumulent les effets issus des modélisations par
éléments finis. Ces valeurs sont toutes ramenées à des valeurs
positives.
Les distributions de densité sont plus sensibles aux variations
finales du module d'Young E.
sont
présentées aux paragraphes précédents par des graphiques qui
traitent de chaque zone pour les densités et de chaque poinçon
pour les efforts. Les valeurs de sensibilité correspondent ainsi
aux pentes de chaque segment de droite.
L'ensemble de ces informations numériques est traité pour obtenir
une présentation synthétique des sensibilités pour chaque cas de
variation.
Ce traitement conduit à exposer les résultats issus des 24
simulations numériques par les quatre figures 7.7.1,
7.7.2, 7.7.3 et 7.7.4. Les valeurs
portées sur ces quatre figures correspondent à des "sensibilités
globales" qui cumulent les effets issus des modélisations par
éléments finis. Ces valeurs sont toutes ramenées à des valeurs
positives.
Les distributions de densité sont plus sensibles aux variations
finales du module d'Young E.
Figure 7.7.1:
Sensibilité des répartitions de densité simulées par
rapport aux paramètres élastiques
|
|
Cette influence majorée des variations finales de E concerne
également les efforts comme le montre la figure 7.7.2.
Figure 7.7.2:
Sensibilité des efforts simulés en fin de compression par
rapport aux paramètres élastiques
|
|
Les variations du coefficient de Poisson ont un impact similaire
au module d'Young soumis à des variations initiales.
Les figures 7.7.3 et 7.7.4 illustrent
respectivement les sensibilités des répartitions de densité et des
efforts par rapport aux variations des paramètres plastiques. La
figure 7.7.4 met en évidence une plus forte sensibilité
globale des quatre paramètres aux variations finales par rapport
aux variations initiales dans le cas des forces simulées en fin de
compression. Pour les répartitions de densité, la figure
7.7.3 indique des sensibilités notables d'ordres de
grandeurs similaires en début et en fin de compression.
Figure 7.7.3:
Sensibilité des répartitions de densité simulées en fin
de compression par rapport aux paramètres
plastiques
|
|
Figure 7.7.4:
Sensibilité des efforts simulés en fin de compression par
rapport aux paramètres plastiques
|
|
Cette étude met en évidence l'influence des paramètres de la loi
de comportement élasto-plastique sur les répartitions de densité
et sur les efforts simulés. Les résultats de cette étude désignent
les paramètres de la loi qui doivent faire l'objet d'une attention
particulière lors de leurs déterminations expérimentales. Parmi
ces paramètres, l'angle de frottement interne  se distingue
par une forte influence de sa valeur aux faibles densités, la
valeur de pression de consolidation
se distingue
par une forte influence de sa valeur aux faibles densités, la
valeur de pression de consolidation  pour son impact aux
fortes densités sur les efforts. La forte sensibilité des
répartitions de densité aux variations finales de l'excentricité
est également à signaler.
Les variations imposées à l'angle de frottement interne
pour son impact aux
fortes densités sur les efforts. La forte sensibilité des
répartitions de densité aux variations finales de l'excentricité
est également à signaler.
Les variations imposées à l'angle de frottement interne  ont une influence importante sur les efforts maximaux simulés en
fin de compression, en particulier lorsque des fluctuations
initiales sont appliquées à ce paramètre.
La densification typique du procédé est essentiellement modélisée,
compte tenu des déformations imposées, par le mécanisme lié à la
surface de charges du Cap plutôt que par le mécanisme inhérent à
la droite de Drucker-Prager. Ainsi, le maintien de fortes valeurs
des sensibilités liées aux variations initiales et finales de
ont une influence importante sur les efforts maximaux simulés en
fin de compression, en particulier lorsque des fluctuations
initiales sont appliquées à ce paramètre.
La densification typique du procédé est essentiellement modélisée,
compte tenu des déformations imposées, par le mécanisme lié à la
surface de charges du Cap plutôt que par le mécanisme inhérent à
la droite de Drucker-Prager. Ainsi, le maintien de fortes valeurs
des sensibilités liées aux variations initiales et finales de
 sont a priori étonnantes. Pour analyser ce résultat, il
convient de reconsidérer les valeurs de sensibilité déterminées
pour le cas simplifié et de développer quelques commentaires
détaillés.
Les tendances exprimées par la figure 7.7.4 correspondent
globalement au cas simplifié, la comparaison avec les sensibilités
en fin de compression de la figure 7.5.4 étant justifiée.
L'influence croissante des paramètres
sont a priori étonnantes. Pour analyser ce résultat, il
convient de reconsidérer les valeurs de sensibilité déterminées
pour le cas simplifié et de développer quelques commentaires
détaillés.
Les tendances exprimées par la figure 7.7.4 correspondent
globalement au cas simplifié, la comparaison avec les sensibilités
en fin de compression de la figure 7.5.4 étant justifiée.
L'influence croissante des paramètres 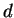 ,
, 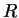 et
et 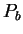 est par
exemple retrouvée. Il demeure que des différences marquées
existent concernant les valeurs de la sensibilité si l'on
considère un à un les effets de chacun des paramètres. Il convient
de rappeler que le cas simplifié ne tient pas compte de la
contribution élastique du comportement et du frottement entre
poudre en outillage. De plus, la géométrie et la cinématique des
outils de la pièce E active le phénomène de transfert de poudre au
cours de la compression. Une dernière différence importante entre
le cas simplifié et les simulations de la pièce E est que le cas
simplifié traite de sensibilité "instantanée" par rapport à la
variable déformation volumique plastique. Le cas simplifié ne met
pas en jeux au cours de la compression simulée l'initiation et le
développement de gradients de densité distincts par application de
variations des paramètres plastiques.
Les éléments finis simulent en moyenne des chemins de contrainte
proches de la compression en matrice. Les éléments finis localisés
à l'angle de la pièce et dans la jupe enregistrent cependant des
histoires de déformation assez distinctes de la compression en
matrice. Ces derniers éléments finis subissent en effet des
chemins de contrainte nettement plus déviatoires en fin de
compression ainsi que l'illustre la figure 7.7.5.
est par
exemple retrouvée. Il demeure que des différences marquées
existent concernant les valeurs de la sensibilité si l'on
considère un à un les effets de chacun des paramètres. Il convient
de rappeler que le cas simplifié ne tient pas compte de la
contribution élastique du comportement et du frottement entre
poudre en outillage. De plus, la géométrie et la cinématique des
outils de la pièce E active le phénomène de transfert de poudre au
cours de la compression. Une dernière différence importante entre
le cas simplifié et les simulations de la pièce E est que le cas
simplifié traite de sensibilité "instantanée" par rapport à la
variable déformation volumique plastique. Le cas simplifié ne met
pas en jeux au cours de la compression simulée l'initiation et le
développement de gradients de densité distincts par application de
variations des paramètres plastiques.
Les éléments finis simulent en moyenne des chemins de contrainte
proches de la compression en matrice. Les éléments finis localisés
à l'angle de la pièce et dans la jupe enregistrent cependant des
histoires de déformation assez distinctes de la compression en
matrice. Ces derniers éléments finis subissent en effet des
chemins de contrainte nettement plus déviatoires en fin de
compression ainsi que l'illustre la figure 7.7.5.
Figure 7.7.5:
Chemin de contrainte dans le plan p-q au cours de la
compression
|
|
Ces chemins déviatoires impliquent une activation du mécanisme lié
à la droite de Drucker-Prager, ce mécanisme étant déterminé par
les paramètres 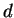 et
et  . Ces paramètres ont alors une
influence sur la répartition de densité qui est pondérée par la
proportion d'éléments finis impliqués. De plus, le coin intérieur
de la pièce est en cisaillement en fin de compression (voir figure
6.3.6) ce qui explique l'influence de la cohésion et de
l'angle de frottement interne en fin de compression. Ainsi,
l'amplitude de ce type d'influence est en rapport direct avec la
géométrie de la pièce et la cinématique de compression.
Cette étude permet également de déterminer les intervalles de
confiance pour les résultats de la simulation en fonction des
incertitudes de mesures expérimentales. A titre d'exemple, des
imprécisions de 10 % pour les paramètres plastiques et de 40%
pour les paramètres élastiques sont considérées. Les erreurs
majorées sur les résultats de la simulation peuvent être déduites,
les valeurs de ces erreurs majorées sont présentées par la figure
7.7.6.
. Ces paramètres ont alors une
influence sur la répartition de densité qui est pondérée par la
proportion d'éléments finis impliqués. De plus, le coin intérieur
de la pièce est en cisaillement en fin de compression (voir figure
6.3.6) ce qui explique l'influence de la cohésion et de
l'angle de frottement interne en fin de compression. Ainsi,
l'amplitude de ce type d'influence est en rapport direct avec la
géométrie de la pièce et la cinématique de compression.
Cette étude permet également de déterminer les intervalles de
confiance pour les résultats de la simulation en fonction des
incertitudes de mesures expérimentales. A titre d'exemple, des
imprécisions de 10 % pour les paramètres plastiques et de 40%
pour les paramètres élastiques sont considérées. Les erreurs
majorées sur les résultats de la simulation peuvent être déduites,
les valeurs de ces erreurs majorées sont présentées par la figure
7.7.6.
Figure 7.7.6:
Erreur relative sur les résultats de simulation
|
|
Cette figure indique que les répartitions de
densité souffrent d'une faible indétermination de l'ordre de
1.3%. En considérant l'erreur relative maximum sur les
répartitions de densité et en l'appliquant aux résultats de la
pièce E de Federal Mogul, on obtient les résultats illustrés par
la figure 7.7.7. Un commentaire important consiste à
rappeler que la validité de cette démarche requiert à la fois des
valeurs de masses volumiques calculées et mesurées
particulièrement précises.
Figure 7.7.7:
Intervalle de confiance sur les masses volumiques
simulées par rapport aux variations de mesures
expérimentales
|
|
L'intervalle d'erreur sur les masses volumiques (induit par les
fluctuations des données) est centré sur les résultats de
simulation. Un fait remarquable à cette figure est que chaque
intervalle ainsi positionné contient les valeurs issues des
mesures expérimentales.
Dans le même esprit, l'erreur maximum pour les forces est
également associée aux résultats de la simulation de la pièce E.
Le résultat est illustré sur la figure 7.7.8.
Figure 7.7.8:
Intervalle de confiance sur les efforts simulées par
rapport aux variations de mesures expérimentales
|
|
L'ensemble des efforts mesurés sont compris dans l'intervalle
d'incertitude de la simulation numérique. Cependant, il apparaît que cet
intervalle d'incertitude sur les efforts est particulièrement important par
rapport aux valeurs même des mesures.




suivant: Conclusion
monter: Étude de sensibilité
précédent: La pression isotrope
Table des matières
FRACHON Arnaud
2002-11-12
![\includegraphics[height=6cm]{syntdensEL.eps}](img903.png)
![\includegraphics[height=6cm]{syntdensEL.eps}](img903.png)
![\includegraphics[height=6cm]{syntfoEL.eps}](img904.png)
![\includegraphics[height=6cm]{syntdensPL.eps}](img905.png)
![\includegraphics[height=6cm]{syntfoPL.eps}](img906.png)
![\includegraphics[width=85mm]{toldens.eps}](img910.png)
![\includegraphics[width=85mm]{tolfor.eps}](img911.png)