



suivant: Schémas implicites
monter: Le code éléments finis
précédent: Introduction
Table des matières
La simulation de la compression des poudres doit prendre en compte
trois facteurs principaux :
- les grands déplacements des outils qui, dans le cadre d'une
description Lagrangienne, induisent de possibles distorsions très
importantes du maillage,
- le frottement entre la poudre et les outils qui est l'une des causes
de l'apparition des gradients de densité,
- l'évolution de la surface de plasticité, caractéristique de l'état du matériau, est déterminée
par des fonctions non-linéaires de la densité.
La combinaison de ces trois facteurs induit une analyse et un
traitement d'un problème fortement non-linéaire. Cette
non-linéarité intervient à la fois aux niveaux de la géométrie,
des déformations et du comportement du matériau. La méthode des
éléments finis permet le traitement de ces non-linéarités. Dans
cette partie, il est proposé un court exposé sur l'essence de
cette méthode et sur les différentes façons de résoudre
numériquement les équations posées par cette méthode.
La méthode des éléments finis repose sur une discrétisation de
l'espace et la résolution des équations d'équilibres (thermique,
mécanique) en des points privilégiés de cet espace. Dans le cas du
procédé de compression à froid, seul l'équilibre mécanique est à
réaliser.
Si l'on ne considère pas les moments volumiques, l'équilibre d'un
corps peut se résumer à la somme des forces de volume et des
forces de contact. Les forces de contact peuvent être exprimées en
fonction du tenseur des contraintes de Cauchy. Le théorème de
Gauss permet de réécrire une intégrale sur une surface en une
intégrale sur un volume, permettant d'écrir qu'un corps est en
équilibre s'il vérifie l'équation 5.2.1.
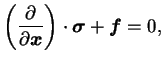 |
(5.32.1) |
où
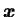 est le champ des coordonnées dans la
configuration actuelle,
est le champ des coordonnées dans la
configuration actuelle,
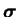 est le tenseur des
contraintes de Cauchy et
est le tenseur des
contraintes de Cauchy et
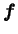 est l'ensemble des forces
de volume (accélération
est l'ensemble des forces
de volume (accélération
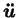 et gravité
et gravité
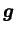 par exemple).
L'équation 5.2.1 est approximée par un
développement au premier ordre. Ceci est obtenu par le produit du
terme de gauche par une fonction test définie et continue sur le
volume puis intégré. Cette formulation dite "faible" (car du
premier ordre) est identifiée au principe des travaux virtuels si
la fonction test est un champ de vitesses virtuelles cinématiquement
admissible. Ce principe est exprimé par l'équation
5.2.2.
par exemple).
L'équation 5.2.1 est approximée par un
développement au premier ordre. Ceci est obtenu par le produit du
terme de gauche par une fonction test définie et continue sur le
volume puis intégré. Cette formulation dite "faible" (car du
premier ordre) est identifiée au principe des travaux virtuels si
la fonction test est un champ de vitesses virtuelles cinématiquement
admissible. Ce principe est exprimé par l'équation
5.2.2.
 |
(5.32.2) |
avec
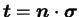 ,
,
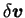 le champ de vitesses virtuelles
cinématiquement admissible et
le champ de vitesses virtuelles
cinématiquement admissible et
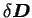 la partie
symétrique du gradient associé à
la partie
symétrique du gradient associé à
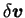 L'espace de l'étude ayant été discrétisé en éléments finis,
l'équation 5.2.2 doit être vérifiée localement pour
chaque n
L'espace de l'étude ayant été discrétisé en éléments finis,
l'équation 5.2.2 doit être vérifiée localement pour
chaque n ud. Dans le cas général des problèmes
non-stationnaires, il est nécessaire dans un premier temps de
discrétiser le problème par rapport au temps puis de résoudre les
systèmes d'équations non-linéaires (en général) résultants qui
sont de la forme
ud. Dans le cas général des problèmes
non-stationnaires, il est nécessaire dans un premier temps de
discrétiser le problème par rapport au temps puis de résoudre les
systèmes d'équations non-linéaires (en général) résultants qui
sont de la forme 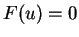 , où
, où 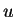 représente les variables
nodales. Dans la suite sont proposées des méthodes de résolution
de ces systèmes.
représente les variables
nodales. Dans la suite sont proposées des méthodes de résolution
de ces systèmes.
Sous-sections




suivant: Schémas implicites
monter: Le code éléments finis
précédent: Introduction
Table des matières
FRACHON Arnaud
2002-11-12
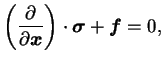
![$\displaystyle \delta \boldsymbol D =
\frac{1}{2}\left(\frac{\partial \delta \b...
...frac{\partial \delta \boldsymbol
v}{\partial \boldsymbol x} \right]^T \right).$](img655.png)