



suivant: Liste des tableaux
monter: aadocmaitre
précédent: Bibliographie
Table des matières
- Des exemples de diverses formes et tailles de grains de
poudre métallique. a) tellurium moulu, aciculaire b) alliage de fer atomisé
avec de l'argon, sphérique avec de fines particules agglomérées, c) tungstène
réduit par gaz, les agrégats sont polygonaux, d) étain atomisé par
air, e) alliage de fer atomisé par centrifugeuse, f) étain éclaboussé trempé,
flocon
- (suite), g) acier inoxydable atomisé par eau, arrondi et irrégulier,
h) palladium par électrolytique, éponge,
i) nickel par décomposition de carbonylique, poreux et cubique, j) verre métallique
à base de fer, ruban écrasé, plats angulaires, k) titane, réduit par sodium moulu,
irrégulier, et l) hydrure de niobium, moulu, anguleux
- Forme des grains de poudres Distaloy AE
- Principe du moulage par injection (MIM)
- Réalisation rapide de prototypes
- Principe de la Compression Isostatique à Chaud
- Principe de la Compression Isostatique à Froid (RIP)
- Principe de la compression par laminage
- Présentation du procédé de mise en forme par
compression-frittage
- Principe de l'atomisation : le métal en fusion est soumis
aux jets d'un fluide qui va isoler les gouttelettes : les
grains
- Écoulement de la poudre lors du remplissage de la
matrice
- La figure de gauche représente la poudre dans la matrice
à la fin du remplissage et la figure de droite représente la
poudre à la fin de la phase de transfert
- Les flèches en noir indiquent le déplacement des outils
lors de la phase de compression. L'absence de flèche indique que
l'outil est fixe.
- Exemple de décharge des outils (flèches vers le haut).
Cela s'accompagne de sollicitations radiales (flèches horizontales)
- Effacement des outils permettant l'éjection de la pièce
- Exemple possible de modification de la géométrie lors de
la phase de frittage
- Presse multi-poinçons
- Cinématique des outils avant pendant et après la compression
- Évolution des efforts sur les poinçons durant et après la compression
- Découpage de la pièce pour les mesures de densité
- Position des défauts sur la pièce.
Ces défauts sont axisymétriques.
- Place de la simulation numérique au sein du processus
d'industrialisation pour la détermination des cinématiques de
compression. Les surfaces fonctionnelles de la pièce et les
épaisseurs qui relient ces surfaces (tenue en service) définissent
des contraintes à prendre en compte
- Place de la simulation numérique au sein du protocole
scientifique de validation de la simulation
numérique
- La pièce à vert n'est qu'un assemblage de grains
- (a) Volume macroscopique représentatif d'un
agrégat de poudre sous chargement axisymétrique (b) Forme
de la surface de charges en fonction des contraintes axiale et
radiale macroscopiques (c) Comparaison de surfaces de
charges pour une distribution isotrope des contacts et le modèle
phénoménologique de CamClay (pointillés) (d)Surface de
charges comparées au critère phénoménologique de Gurson
(pointillés) pour différentes densités relatives
D.
- Mesure de la déformation en fonction de la contrainte
appliquée
- Espace des contraintes principales dans lequel est représenté un plan
contraintes isotropes-contraintes équivalentes de Von Mises.
- Boîte triaxiale, les trois directions sont indépendantes
(à gauche) ; mesures possibles par ce dispositif (à droite)
- Triaxiale de révolution (à gauche), les deux directions radiales
sont identiques ; une interprétation possible d'essais réalisés par
ce dispositif
- Principe de l'essai de densification en matrices (à droite). Chemin
de contraintes pour la densification d'une poudre de fer (à
gauche)
- Le comprimé de poudre frotte sur une règle dont le déplacement est piloté
- Cisaillement, où l'entre-fer n'est pas nul
- Traction uniaxiale (à gauche) ; possibilité de mesurer la
contrainte de rupture par ce dispositif
- Compression uniaxiale d'un échantillon de section
circulaire (à gauche). La section peut également être rectangulaire.
Évolution de la déformation volumique au cours de cet essai
- Compression diamétrale ou essai brésilien (à gauche) ;
mesure de la contrainte de rupture (à droite)
- Représentation des chemins de contraintes pour la
compression en matrice, la compression diamétrale, la
compression uniaxiale et la traction uniaxiale dans un plan p-q
- Représentation des chemins de contraintes
possibles avec le dispositif de compression triaxiale de
révolution dans un plan p-q
- Résultats de la compression dométrique dans un plan
p-q
- Repérage d'une densité de comprimé pour une compression
dométrique.
- Deux densités de comprimés de 6.5 et 7.1 pour un chemin
dométrique et par des chemins triaxiaux de
révolution
- Évolution du seuil de plasticité par rapport à la
densité relative pour un comprimé obtenu par compression isotrope
(A) [RCR01]
- Évolution de la limite élastique en fonction de la
densité relative pour un échantillon mis en forme par compression
en matrices (B) [RCR01]
- Évolution du rapport
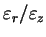 au
cours de la compression isotrope [RCR01]
au
cours de la compression isotrope [RCR01]
- Limites élastiques pour des essais normalement consolidés
et sur-consolidés
- Compression uniaxiale monotone sur des comprimés de mises
en forme différente (en matrices et isotrope). Figure issue de la
thèse de P. Mosbah
- Compression uniaxiale monotone sur un comprimé mis en
forme en matrice et testé suivant deux directions
- Évolution de la contrainte de rupture en fonction de la
masse volumique pour une poudre de fer
- Fabrication de l'échantillon dans une matrice de section
carrée
- Compression uniaxiale dans la direction de fabrication de
l'échantillon et dans la direction orthogonale
- Réponse dans un diagramme contrainte-déformation aux
sollicitations cycliques
- Suppression de l'enveloppe élasto-plastique
- Diagramme déformation élastique-contrainte mettant en
évidence la superposition des cycles
- Réponse axiale pour une densité de

- Réponse axiale pour une densité de
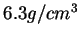
- Réponse axiale pour une densité de
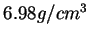
- Évolution de la raideur (module d'Young) et de la masse
volumique en fonction de la pression appliquée lors d'une
compression dométrique par Dawson &
al.
- Évolution de la forme des grains au cours de la
compression en matrice. (A) au remplissage, (B) en cours de
compression, (C) densification complète
- Erreur
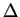 pour un même niveau de contrainte entre
un modèle élastique linéaire et non-linéaire
pour un même niveau de contrainte entre
un modèle élastique linéaire et non-linéaire
- Chemins de contraintes en charge et en décharge
- Comparaison entre le modèle de Lade calé pour la poudre de fer
et les données expérimentales obtenues par compression uniaxiale
- chemins de contraintes en charge et en décharge
- Pour les faibles niveaux de contraintes, il y a une
partie non-linéaire, puis une partie linéaire pour des contraintes
plus importantes
- comparaison entre les données expérimentales
et le modèle pour une densité de 5.84
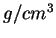
- comparaison entre les données expérimentales
et le modèle pour une densité de 6.30
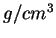
- comparaison entre les données expérimentales
et le modèle pour une densité de 6.98
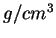
- Évolution de la forme des grains au cours de la
compression en matrice ainsi que de la surface de contact entre
grains. (A) au remplissage, (B) en cours de compression, (C)
densification complète
- Décomposition du comportement par le partitionnement de la
déformation en une partie élastique et une partie plastique et évolution
du seuil plastique
- Transformation au cours du temps
- La dérivée partielle du potentiel g par rapport aux contraintes
est la normale à une surface définie par l'ensemble des états de
contraintes ayant une même valeur du potentiel
- Représentation du critère de CamClay initial dans un plan p-q
- Représentation du critère de CamClay modifié dans un plan p-q
- Représentation du critère de CamClay dans l'espace des contraintes
principales
- Représentation du critère de CamClay dans le plan contrainte
isotrope(p)- contrainte déviatoire (q)
- Représentation des surfaces de charges pour le modèle de Drucker-Prager/Cap
dans le plan des contraintes isotropes (p) contraintes déviatoires (q)
- Représentation des surfaces de charge pour le modèle de Drucker-Prager/Cap
dans l'espace des contraintes principales
- Représentation des potentiels d'écoulement dans un plan p-q
- Pour des géométries complexes telles que celles des grains
de poudre de fer, la normale au contact ne coïncide pas nécessairement
avec la jonction des centres. Pour des sphères, cette coïncidence est
systématique
- Évolution de la forme des grains au cours de la
compression en matrice. (A) au remplissage, (B) en cours de
compression, (C) densification complète
- Transformation de l'espace des contraintes afin d'exprimer
le critère de plasticité sous une forme isotrope
- Surface de charge pour une consolidation isotrope
- Surface de charge pour une consolidation anisotrope
- Surface de charge pour une consolidation anisotrope
- L'espace des contraintes "réelles" (à gauche) est transformé
en un espace des contraintes "normalisées" (à droite)
- Modification de l'espace des contraintes par la prise en compte de
l'écrouissage cinématique
- Modification de l'espace des contraintes par la prise en compte de
l'écrouissage isotrope
- Modification de l'espace des contraintes par la prise en compte de
l'écrouissage tournant
- Points d'iso-densités dans un espace des contraintes
p-q pour différentes poudres résultant d'essais de compression
triaxial
- Points d'iso-densités dans un espace des contraintes
(
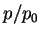 )-(
)-(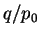 ) pour différentes poudres résultant d'essais
de compression triaxial
) pour différentes poudres résultant d'essais
de compression triaxial
- Évolution de la surface de charges selon que la sollicitation
est déviatoire (à gauche) ou isotrope (à droite)
- Illustration du schéma implicite d'intégration au cours
du temps
- Illustration de la méthode de Newton
- Illustration du schéma explicite d'intégration au cours
du temps
- Illustration de l'opérateur de différence centrale
- Contact entre une surface maître et une surface esclave
- Évolution de la distorsion
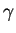 en fonction de la
contrainte de cisaillement
en fonction de la
contrainte de cisaillement 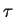
- Décomposition de l'état de contrainte à l'interface
en une contrainte normale
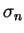 et une contrainte tangentielle
et une contrainte tangentielle
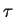
- Illustration de la méthode prédiction élastique-correction
plastique
- Effet sablier : les éléments se déforment à volume
constant
- Évolution du module d'Young (E) en fonction de la
déformation volumique plastique
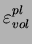 pour
une masse volumique initiale
pour
une masse volumique initiale

- Calage de la surface de Drucker/Prager par l'essai de
traction uniaxiale (à gauche) et l'essais de de compression uniaxiale
(à droite) dans le plan P-Q
- Résultats de mesure pour caler les paramètres de la
droite de rupture avec contrainte de rupture en traction uniaxiale (à droite)
et évolution de la cohésion d déduite des données expérimentales (à gauche).
(
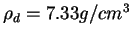 )
)
- Calage de la surface de charge (iso-densité) dans un plan
p-q à partir d'essais de compression triaxiale normalement
consolidés
- Évolution des paramètres de la surface de charge en
fonction de la déformation volumique plastique
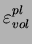 pour une masse volumique initiale de
pour une masse volumique initiale de
 .
(a)cohésion d (b) angle de frottement
interne
.
(a)cohésion d (b) angle de frottement
interne  (c) excentricité R (d) pression isotrope
(écrouissage)
(c) excentricité R (d) pression isotrope
(écrouissage) 
- Calage de la surface du Cap en fonction de la densité au
point d'intersection avec le chemin de chargement (normale à la
surface de pente 2/3)
- Chemin de contrainte dans un plan P-Q pour les trois
centres de recherches
- Évolution de l'excentricité du cap
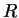 en fonction
de la masse volumique
en fonction
de la masse volumique
- Évolution de la pression de consolidation
 en
fonction de la masse volumique
en
fonction de la masse volumique
- Evolution de la pente d'état critique M en
fonction de la densité
- Evolution de la pression de consolidation
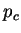 en
fonction de la densité
en
fonction de la densité
- Faisceau d'iso-masse volumique pour les surfaces de
charge du modèle de CamClay
- Forme générique des pièces réalisées sur presse instrumentée
de la société Federal Mogul
- Les cinq zones de mesure de la densité et les dimensions
caractéristiques de la pièce
- Maillage de la pièce en L pour la cinématique E
- Définition des deux colonnes et vitesses de compression respectives
au cours du temps
- Résultats de la répartition de densités dans la pièce E
- Extraction des déformations volumiques plastiques dues au mécanisme de
Drucker/Prager. Formation envisageable de la fissure pendant la phase de
compression de la pièce E
- État de contraintes dans la pièce E : pression isotrope (à gauche)
et contraintes équivalente de Von Mises (à droite)
- État de contraintes dans la pièce E : contraintes
axiales
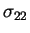 (à gauche) et les contraintes de
cisaillement
(à gauche) et les contraintes de
cisaillement
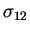 (à droite)
(à droite)
- État de contraintes dans la pièce E : contraintes radiales
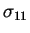 (à gauche) et les contraintes orthoradiales
(à gauche) et les contraintes orthoradiales
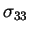 (à
droite)
(à
droite)
- Maillage de la pièce en L pour la cinématique B : avec
des outils rigides (à gauche) ou des outils élastique (à
droite)
- Résultats de la répartition des masses volumiques dans la pièce B
en fin de compression
- État de contraintes dans la pièce B pour le modèle éléments finis
1 : pression isotrope (à gauche) et contrainte équivalente de Von
Mises (à droite)
- Résultats de la répartition de densité dans la pièce B
suite à l'éjection avec une contre-force
- Résultats de la répartition de densité dans la pièce B
suite à l'éjection sans contre-force
- État de contraintes dans la pièce B pour le modèle éléments finis
2 : pression isotrope (à gauche) et contraintes équivalente de Von
Mises (à droite)
- résultats de la répartition de densités dans la pièce 21
avec le modèle intégré de CamClay
- État de contraintes dans la pièce B pour le modèle éléments finis
3 : pression isotrope (à gauche) et contraintes équivalente de Von
Mises (à droite)
- Dimensions des outils élastiques intégrés à la simulation numérique.
Module d'Young 210 GPa et coefficient de Poisson 0.3
- Résultats de la répartition de masse volumique dans la pièce B
pour les conditions de simulation n^&cir#circ;4, suite à l'éjection
- État de contraintes dans la pièce B pour le modèle éléments finis
4 : pression isotrope (à gauche) et contraintes équivalente de Von
Mises (à droite)
- Forme de la pièce mise en forme par la société DORST
- Valeurs des rayons et découpage de la section de la pièce en sept zones
- Mise en relief d'un transfert de poudre possible entre colonnes
par observation du taux de compression de chaque colonne.
- Maillages pour les deux modèles éléments finis de la
pièce Dorst : outils rigides sans remaillage de la poudre (à gauche) et outils
élastiques poudre remaillée (à droite)
- Répartition de densité dans la pièce Dorst d'après la simulation numérique (à gauche) et les mesures par zones (à droite) avec des outils rigides et un modèle de Drucker-Prager/Cap pour la poudre
- Comparaison entre l'expérience et la simulation
numérique pour les répartitions de densités pour les zones 1 à 7
- Résultats de la simulation numérique pour les efforts
en fin de compression
- Comparaison entre la mesure expérimentale et les
résultats de simulation associés à la somme des efforts des
poinçons supérieurs
- Vis-à-vis entre écarts de densité (dans les zones) et
valeurs d'efforts (sur les poinçons) pour les trois centre : 3S (à
gauche), Leicester (au centre) et AEA (à droite)
- État de contraintes dans la pièce : pression isotrope
(à gauche) et contrainte équivalente de Von Mises (à droite)
- Répartition des masses volumiques simulées pour la pièce Dorst (à gauche) et mesures par zone
(à droite) avec des outils élastiques et le modèle de CamClay.
- Principe de variation arbitraire des paramètres en
fonction de la déformation volumique plastique au stade initiale
(à gauche) et au stade final (à droite)
- Variation du module d'Young en début de compression (à
gauche) et en fin de compression (à droite)
- Variation de la cohésion pour les faibles (à gauche) et
pour les fortes (à droite) déformations volumiques
- Variation de l'angle de frottement interne pour les
faibles (à gauche) et pour les fortes (à droite) déformation
volumique
- Variation de l'excentricité pour les faibles (à gauche)
et pour les fortes (à droite) déformations volumiques
- Représentation de l'effet des variations de
l'excentricité R dans le plan P-Q en fin de compression
- Variation de la pression isotrope pour les faibles (à
gauche) et pour les fortes (à droite) déformations volumiques
- Évolutions de la sensibilité de la contrainte de
compression par rapport aux paramètres plastiques au cours de la
compression
- Chemins de contraintes dans des plans p-q pour une
variation imposée en fin de compression à chaque paramètre
plastique
- Sensibilité de la contrainte au cours de la compression
par rapport aux variations des paramètres plastiques présentées en
début de chapitre
- Sensibilité de la contrainte axiale en début et en fin de
compression par rapport aux variations numériques imposées aux
paramètres plastiques
- Résultats de la sensibilité des répartitions de densités
et des efforts par rapport aux variations relatives du module
d'Young au stade initial et au stade final
- Résultats de la sensibilité des répartitions de densités
et des efforts par rapport aux variations relatives du coefficient
de Poisson
- Résultats de la sensibilité des répartitions de densité
et des efforts par rapport aux variations relatives de la cohésion
au stade initial et au stade final
- Résultats de la sensibilité des répartitions de densité
et des efforts par rapport aux variations relatives du coefficient
de frottement interne au stade initial et au stade
final
- Modification schématique de la surface du Cap lorsque
l'angle de frottement interne varie. La flèche symbolise la
direction de l'écoulement plastique
- Résultats de la sensibilité des répartitions de densité
et des efforts par rapport aux variations relatives de
l'excentricité au stade initial et au stade final
- Résultats de la sensibilité des répartitions de densité
et des efforts par rapport aux variations relatives de la pression
isotrope de consolidation au stade initial et au stade
final
- Sensibilité des répartitions de densité simulées par
rapport aux paramètres élastiques
- Sensibilité des efforts simulés en fin de compression par
rapport aux paramètres élastiques
- Sensibilité des répartitions de densité simulées en fin
de compression par rapport aux paramètres
plastiques
- Sensibilité des efforts simulés en fin de compression par
rapport aux paramètres plastiques
- Chemin de contrainte dans le plan p-q au cours de la
compression
- Erreur relative sur les résultats de simulation
- Intervalle de confiance sur les masses volumiques
simulées par rapport aux variations de mesures
expérimentales
- Intervalle de confiance sur les efforts simulées par
rapport aux variations de mesures expérimentales
FRACHON Arnaud
2002-11-12